Раскрытие круга и человечек на стене.
Словосочетание “раскрытие круга” многих смутило и ввело в непонятки.
Я былоче попробовал нагуглить любимый мной “куб окружностей”, и ирокезик на мне поставился сам собой. Его либо нет в учебниках по рисованию, либо, лучше бы не было. Древнее искусство строить окружность в перспективе, почти утеряно, мать вашу. Со мной оно уйдет! Я должен подготовить приемника!
Узри же!
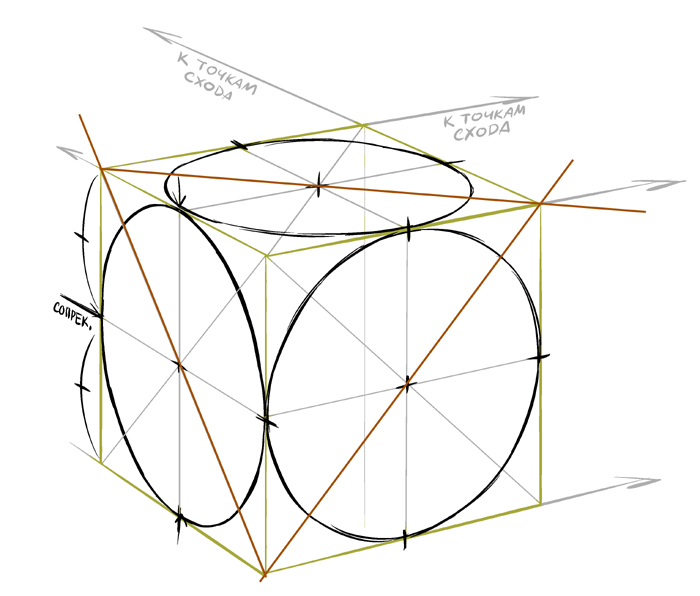
Ну на самом деле ничего сакрального, конечно. Но глядя на то сколь многие учебники учат рисовать круги “рыбкой”, и сколь многие, хорошие, художники эти “рыбки” потом старательно переносят в свои работы, не мог не содрогнуться, и не нарисовать этот кубик. Встраивая в него окружность, вы легко понимаете как он потом на плоскости то мнется.
Обычно его рисуют семитричным, но для наших целей наглядней вот так.
Кубик с точками схода построить может каждый, ну а дальше все просто. Центральные осьи и у кругов и у сторон куба совпадают, и найти его не трудно, как видите. Соприкасаются круги и квадраты в одном и том же месте, посередь стороны квадрата. А коричневые линии символизируют тут наклон круга, самое его широкое место при сплющивании (Долгое и интересное обсуждение выявило, что строго говоря это не так, и наиболее широк сплюснутый круг по линии перпендикулярной оси стороны куба, хоть при рисовании все же удобней набрасывать по диагонали ^___-)). В точки пересечения линии и круга и приходит сторона всего цилиндрического с этим кругом в основании.
Как видите не высшая математика.)
А вот сплющивание круга, от приближения его к уровню линии горизонта, и соответственно собственной двухмерности, и носит название “раскрытие круга”. Чем ниже-выше, тем больше круг, чем посерёдней, тем больше “линия”.
Проиллюстрировано это картинкой к восхитительной книжки “Человечек на стене” А. Воловика.>>>>
Если вы её в детстве не читали, прочитайте сейчас. Если у вас есть дети, прочитайте им. Роль этой книги в воспитании художника из, например, меня, переоценить трудно. Так что делайте выводы.)

 99) Френдлента
99) Френдлента









(Шепотом)
Даниил Анатольевич, это забытое знание находится на 55-57 странице канонического учебника “Рисунок” из серии “Специальность Архитектура”. Книжка регулярно переиздается уже лет 20.
Пасиба
>Даниил Анатольевич, это забытое знание находится на 55-57 странице канонического учебника “Рисунок
Тоже, да не тоже. там не слишком внятно изображено.
>нет в учебниках по рисованию
А вот учебник черчения в этом вопросе вполне подробен, как мне кажется – http://www.stroyka.ru/Materials/1764/1575564/cherchenie/?BOOK_ID=4383&ID=1575564&strict=N&new=Y
Спасибо! )
При попытке отыскать элементарное в еинете натыкаюсь всюду на раскрытие убийства м-круга……. Даже не смешно
на иллюстрации самый верхний круг – таки немножко рыбкой ))
>А вот учебник черчения
Так, да ни так. Дело в том что несмотря на верное вписывания, для рисования неверно отображено само построение куба. Естественно все типы изометрии идут лесом. Двумерную проекцию можно учитывать, но помнить об отсутствии точек схода.
>натыкаюсь всюду на раскрытие убийства м-круга……. Даже не смешно
Ха, а я успел пошуть об этом в жж.)
Возможно я ляпну ересь, но. А не проще и практичнее использовать для этих целей средства трёхмерного моделирования? В любой программе накидать кубиков и цилиндров дело 1-5 минут. Снять скриншот и сверху рисовать. Нет?
“Иногда тупо нету разетки “
Это не ересь, только если ты технарь и целью являются точные круги и кубики. А именно рисование с такой подготовкой монтируется слабо.
А меня этому сакральному знанию научили на курсах в Рериха х)) Ну, как научили – показали как надо, и я стараюсь именно вот так. Вообще походу это реально сакральное знание, если я после стольких лет в художках это только в девятом классе узнала.(
А что значит “рыбкой”? Я как раз этого не знаю.
“рыбкой” это когда по краям у перспективно сокращенной окружности острые углы. выходит такое “веретено”, схематическая рыбка без хвоста. как правило так лажаются когда раскрытие окружности скрыто плоскостью. например на нижнем основании цилиндра, но некоторые могут постараться и нарисовать так и открытую верхнюю плоскость.
А, понятно, как раз на днях одного юношу пришлось от этого отучать.
Вот теперь читаю “Человечка на стене”. Блин, впервые обратил внимание, что картина “Не ждали” нарисована с точки зрения человека, сидящего в комнате.
http://artdesign21.narod.ru/img/esher/38.jpg
хе-хе
Так меня в свое время и учил матар. Жаль, я забыл, потом самому вспоминать пришлось.
Даниил, диагональ стороны куба (те самые коричневые линии) ну ни разу не должны совпадать с большой полуосью эллипса, в который превращается круг при проекции. Это легко проверить, представив этот самый куб повернутым вокруг вертикальной оси гранью к зрителю. По вашей логике, в таком ракурсе эллипс вообще должен быть наклонным, несмотря на то, что куб стоит вертикально.
С тем, что “рыбка” – это пиздец, я согласен, но зачем вводить народ в другое заблуждение?
> эллипс вообще должен быть наклонным
я имею в виду эллипс на верхней грани куба
Стоп. Оставим в стороне что круг в элипс, строго говоря не привращаеться. Гораздо важнее понять, что такое “полуось”, в данном случае. Радиус чтоли? Так что хрен поймешь чего мы пытаемся проверить вертя куб.
Я опечатался. Имелись в виду конечно же оси ).
Большая ось – отрезок проходящий через самое широкое место эллипса. Малая ось – отрезок проходящий через самое узкое (а полуоси соответствуют длинам отрезков этих осей от центра до края эллипса; это понятие вообще больше к математике имеет отношение, так что не будем его рассматривать сейчас).
Вертя куб, я хотел добиться ракурса, при котором наглядно видно что диагональ грани не соответствует наклону большой оси эллипса.
Вот, постарался в Пайнте изобразить то, о чём хотел сказать:
[URL=http://saveimg.ru/show-image.php?id=c10d1a4ebb460f6f69058b25335afe88] [IMG]http://saveimg.ru/thumbnails/18-12-13/1173d3417ca76476c2f87960d1f2ac74.png[/IMG][/URL]
Я уже вижу новый пост специально по этой теме. Так что продублирую комментарий пожалуй ещё и туда ).